Plus de détails
Tout au long des siècles, les rapports entre les arts et les mathématiques dans le monde occidental furent fréquents. Parfois les mathématiques offrirent un langage permettant de décrire et de mieux comprendre certains aspects des arts ; parfois, au contraire, les arts introduisirent d’eux-mêmes des éléments mathématiques. Il arrive que ce dialogue interdisciplinaire s’inscrive au sein même de l’esthétique artistique.Le lien entre musique, danse et mathématiques se retrouve également dans des questions esthétiques, compositionnelles et chorégraphiques. Pour accéder au dossier complet : Musique, danse et mathématiques
 La musique a été considérée par les Anciens comme un art libéral, au même titre que l'arithmétique. Cet article se propose d'explorer un exemple concret où le raisonnement mathématique permet de répondre à une question musicale : celle du dénombrement des modes à transposition limitée.
La musique a été considérée par les Anciens comme un art libéral, au même titre que l'arithmétique. Cet article se propose d'explorer un exemple concret où le raisonnement mathématique permet de répondre à une question musicale : celle du dénombrement des modes à transposition limitée.
Qu'est-ce qu'un mode ? Il s'agit d'une division de l'octave en un certain nombre de hauteurs, séparées entre elles par des intervalles bien choisis. Le majeur ou le mineur, par exemple, sont des modes célèbres car ils sont au fondement du système tonal ; on parle de do majeur quand l'octave do–do est divisée selon le mode majeur, ou de fa mineur quand l'octave fa–fa est divisée selon le mode mineur.
Une octave est couramment divisée en 12 demi-tons égaux : ces demi-tons constituent en quelque sorte l'intervalle élémentaire de la musique occidentale, et même si certains compositeurs du XXe siècle ont utilisé d'autres subdivisions (Maurice Ohana et les tiers de ton, ou Ivan Wyschnegradsky et les quarts de ton, pour ne citer qu'eux), nous nous placerons dans ce cadre d'étude. De la sorte, on symbolise un mode par une suite de chiffres qui donnent le nombre de demi-tons entre deux notes successives. Par exemple, le mode majeur est décrit par
2 2 1 2 2 2 1
On peut vérifier que la somme des chiffres d'un mode vaut 12, soit le nombre total de demi-tons nécessaire au franchissement d'une octave.

La gamme de do majeur
En musique, depuis le plain-chant, les modes correspondent à un ethos, une atmosphère, un caractère, dont le langage ordinaire ne suffit pas à rendre compte de façon univoque, mais en vertu desquels l'oreille reconnaît le mode quelle que soit l'octave qu'il divise. Autrement dit, d'un point de vue musical, le mode est plus déterminant que la hauteur. Si la fantaisie nous en prenait, on pourrait parfaitement transposer la Sonate Pathétique de Beethoven de do mineur en ré mineur, et elle resterait reconnaissable. Mais on ne pourrait pas la transposer de do mineur en do majeur sans la dénaturer entièrement. Cela explique l'attachement des compositeurs pour les modes et, surtout à la fin du XIXe siècle et au début du XXe, leurs efforts pour en découvrir de nouveaux et les utiliser, afin de diversifier le langage musical. On peut mentionner la redécouverte des modes anciens autour de l'école Niedermeyer de Paris, et l'utilisation qu'en fit Gabriel Fauré dans sa propre musique.
Demandons-nous ce qu'il se passe lorsque nous transposons un mode, c'est-à-dire lorsque nous changeons l'octave qu'il divise (ou sa « note de départ »). Puisqu'il existe douze notes de départ possible (do, do dièse ou ré bémol, ré, ré dièse ou mi bémol, etc.), nous obtenons douze choix de transposition possibles, et a priori, à chaque transposition, une sélection différente de notes parmi les douze qui existent. C'est bien le cas pour les modes majeurs et mineurs : c'est justement pourquoi il existe douze tonalités majeures et douze tonalités mineures différentes, et pourquoi les grands cycles fameux de l'histoire de la musique comportent vingt-quatre pièces dans tous les tons, du Clavier bien tempéré de Johann Sebastian Bach aux Préludes et Fugues op. 87 de Dimitri Chostakovitch, en passant par les Préludes de Chopin et de Rachmaninov.
Olivier Messiaen, dans Technique de mon langage musical, se pose pourtant une question simple, que nous allons reprendre à notre compte : existe-t-il des modes qui possèdent moins de douze transpositions différentes (indépendamment de l'ordre des notes qu'ils contiennent) ? Si oui, combien ? Une première réponse est qu'il existe déjà le « total chromatique », c'est-à-dire le mode composé de tous les demi-tons :
1 1 1 1 1 1 1 1 1 1 1 1
Ce mode contient la totalité des notes, et donc ne change pas quelle que soit la note d'où l'on parte ; mais on peut considérer qu'il ne s'agit pas véritablement d'un « mode », puisque constituer un mode consiste tout autant à choisir certaines notes qu'à renoncer à d'autres : la poésie de la sonorité ou de la couleur d'une gamme viennent en partie du fait que certaines notes sont absentes, et permettent qu'entre celles qui sont présentes se tisse une cohérence sonore.
Messiaen, pour sa part, répond qu'en dehors du total chromatique, il existe sept tels modes, qu'il classifie et dénomme « modes à transposition limitée ». Arrêtons-nous, à titre d'exemple, sur les premiers de ces modes. Le mode I est plus connu sous son nom de « gamme par tons ». Il contient six notes, et s'écrit, dans notre codification,
2 2 2 2 2 2
Cette gamme est célèbre pour avoir été employée de façon systématique par Claude Debussy – comme cas d'école, songeons à Voiles, l'un des Préludes pour piano. Or cette gamme, on le vérifie, ne possède que deux transpositions différentes : que nous partions de do ou de ré, par exemple, les mêmes notes seront effleurées. Voici les deux seules transpositions de ce mode :

La gamme par tons (ou mode I de Messiaen)
Quant au mode II, parfois appelé « mode octotonique » (à huit notes), il fut très en vogue au début du XXe siècle, notamment parmi les héritiers de César Franck. On en trouve un exemple particulièrement développé dans la dernière des Trois danses symphoniques op. 6 de Maurice Duruflé. Ce mode consiste en une alternance rigoureuse de demi-tons et de tons :
1 2 1 2 1 2 1 2
et il possède trois transpositions.

Le mode octotonique (ou mode II de Messiaen)
Le but de cet article est de montrer mathématiquement qu'on peut dénombrer en réalité neuf modes à transposition limitée, et que Messiaen en a omis certains, peut-être au nom d'un attrait mystique pour le nombre sept. Mais pour attaquer mathématiquement le problème, nous devons formaliser la question et en préciser les contours. Que cherchons-nous exactement ? D'un point de vue mathématique, nous sommes en fait en train de chercher certaines partitions ordonnées de 12. Si n est un entier, on appelle partition de n (au sens étymologique de « découpage ») une liste d'entiers dont la somme vaut n. Par exemple,
1 1 1 3 ou 2 4
sont des partitions de 6, c'est-à-dire des façons de diviser 6 en sous-unités plus petites. On dit qu'une partition est ordonnée lorsque l'ordre de ces sous-unités est pris en compte, et que l'on choisit de différencier
1 3 1 1 et 1 1 1 3
par exemple. Dans le cas d'un mode, c'est effectivement ce que l'on cherche : répartir les douze demi-tons en petits intervalles, dont l'ordre importe. Il y a une restriction toutefois : on ne peut considérer qu'une partition est un mode que si elle comporte suffisamment de notes. Par exemple,
6 6
est une partition de 12, mais elle ne contient que deux notes, et n'est donc pas vraiment un mode, une gamme sur laquelle on peut construire un univers sonore et harmonique. Par convention, on considérera donc qu'une partition n'est un mode que si elle contient au moins 5 notes, par référence au mode pentatonique (que l'on entend par exemple dans Laideronnette, Impératrice des Pagodes, de Maurice Ravel, et qui suffit véritablement à donner quant à lui une sensation modale).
Une remarque en passant : une permutation circulaire d'un mode ne donne pas un nouveau mode, mais seulement une transposition du même mode. On appelle permutation circulaire d'un mode l'opération qui consiste à couper le mode en deux parties et à les échanger. Par exemple,
2 2 1 2 2|2 1 et 2 1|2 2 1 2 2
sont en réalité le même mode majeur : le deuxième n'est qu'une transposition du premier (si l'on part sur do, il encodera la gamme de mi bémol majeur).
À présent, observons qu'on peut construire des modes par répétition d'une même cellule. Si d est un diviseur strict de 12 (c'est-à-dire 1, 2, 3, 4 ou 6), en se donnant une partition de d et en la répétant assez, on construit une partition ordonnée de 12. Donnons un exemple :
1 1 2
est une partition de 4. On peut donc construire un mode en répétant 3 fois cette partition, de la façon suivante :
1 1 2|1 1 2|1 1 2
Les modes ainsi obtenus revêtent par construction un aspect symétrique, c'est pourquoi on les appelle, pour simplifier, les partitions périodiques de 12.
Énonçons donc le théorème que nous allons prouver :
Théorème : Les modes à transposition limitée sont exactement donnés par les partitions périodiques de 12.
Ce théorème est un théorème exhaustif (ou de classification) : il s'agit donc de prouver à la fois
a) qu'un mode à transposition limitée s'écrit de façon périodique ;
b) qu'une partition périodique encode un mode qui possède au plus 11 transpositions différentes.
Prouvons d'abord le point b), qui est plus simple. Soit d un diviseur strict de 12, et une partition construite par répétition d'une partition de d. Si l'on transpose le mode de d demi-tons vers le haut (c'est-à-dire que l'on commence le mode au début du 2e segment), on trouve, par définition, exactement les mêmes notes, puisqu'on construit le mode par la même succession d'intervalles. On a donc bien prouvé que l'une au moins des transposition du mode contient les mêmes notes qu'au départ, et donc que la partition considérée encode un mode à transposition limitée.
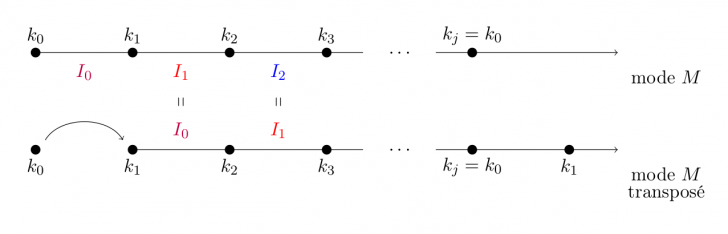
Prouvons maintenant le point a). Si M est un mode à transposition limitée, notons k0 sa note de départ, et k1 la première note telle qu'en commençant le mode M sur k1, on obtienne les mêmes notes qu'en le commençant sur k0. Alors nécessairement, la suite d'intervalles compris entre k0 et k1 (que l'on notera I0) se répète aussi de k1 jusqu'à une certaine note k2, et ainsi de suite, jusqu'à une certaine note kj qui est de nouveau k0. Le mode M est donc composé de j fois la même séquence de demi-tons I0. Il est donc codé par une partition périodique de 12 (dont la cellule de base est de longueur le nombre total de demi-tons contenus dans I0). Le schéma suivant récapitule le raisonnement que nous venons de faire :
En notant que le nombre de transpositions possibles du mode M est donné par la longueur de I0, on déduit comme corollaire de ce théorème qu'un mode à transposition limité ne peut admettre que 1, 2, 3, 4 ou 6 versions différentes (c'est-à-dire un diviseur strict de 12). En particulier, il n'existe pas de mode n'ayant que 5 transpositions possibles. De même, si l'on avait divisé l'octave en, non pas 12, mais p intervalles élémentaires, avec p un nombre premier, il n'existerait pas de modes à transposition limitée (car p admet 1 pour seul diviseur strict, et il n'existerait donc que le total chromatique).
Le théorème permet donc de classifier tous les modes à transposition limitée, ce que nous faisons dans le tableau suivant :
| Diviseur strict | Partition élémentaire | Partition de 12 | Nom chez Messiaen |
|---|---|---|---|
| 1 | 1 | 1 1 1 1 1 1 1 1 1 1 1 1 | [total chromatique] |
| 2 | 2 | 2 2 2 2 2 2 | mode I |
| 3 | 1 2 | 1 2 1 2 1 2 1 2 | mode II |
| 4 | 1 1 2 | 1 1 2 1 1 2 1 1 2 | mode III |
| 1 3 | 1 3 1 3 1 3 | absent chez Messiaen | |
| 6 | 1 1 1 1 2 | 1 1 1 1 2 1 1 1 1 2 | mode VII |
| 1 1 1 3 | 1 1 1 3 1 1 1 3 | mode IV | |
| 1 2 3 | 1 2 3 1 2 3 | absent chez Messiaen | |
| 1 1 4 | 1 1 4 1 1 4 | mode V | |
| 1 1 2 2 | 1 1 2 2 1 1 2 2 | mode VI |
Notons que l'on a supprimé de ce tableau, comme annoncé au début, les modes comportant moins de cinq notes (tels 3 3 3 3 ou 2 4 2 4).
Pour conclure, signalons que les mathématiciens se sont beaucoup intéressés aux partitions des nombres entiers, en particulier à la question de leur nombre : combien y a-t-il de manières d'écrire n comme une somme d'entiers plus petits (sans prendre en compte leur ordre, cette fois) ? On appelle ce nombre p(n). En 1918, c'est-à-dire il y a précisément un siècle, alors que mouraient Debussy et Lili Boulanger, le mathématicien britannique Godfrey Harold Hardy et son protégé indien Srinivasa Ramanujan sont parvenus à donner une formule approchée pour p(n) lorsque n devient très grand. Ce progrès majeur a permis dans son sillage d'importantes avancées mathématiques.
Crédits photographiques : Olivier Messiaen © Roger Picard
Plus de détails
Tout au long des siècles, les rapports entre les arts et les mathématiques dans le monde occidental furent fréquents. Parfois les mathématiques offrirent un langage permettant de décrire et de mieux comprendre certains aspects des arts ; parfois, au contraire, les arts introduisirent d’eux-mêmes des éléments mathématiques. Il arrive que ce dialogue interdisciplinaire s’inscrive au sein même de l’esthétique artistique.Le lien entre musique, danse et mathématiques se retrouve également dans des questions esthétiques, compositionnelles et chorégraphiques. Pour accéder au dossier complet : Musique, danse et mathématiques